Lacan was a visual thinker. This is not the application of a worn cliché but rather a resuscitation of what it means to be a visual thinker. In his annual lectures, particularly in the group of lectures called “the middle lectures” (Seminars IX—XIV?), Lacan not only talks in terms of spatio-temporal experience and visual examples, especially paintings (Velázquez, Balthus, Holbein, Magritte), but he employsy projective geometry not just as a way to find analogies to conditions of the psyche, but as the actual “effective form” of the psyche, as if to live out the destiny of Freud’s enigmatic note of 1938, “Psyche is extended, knows nothing of it.”

For Lacan, psyche is not just extended, it is extension, and the rules of that extension were discovered by Pappus of Alexandria in 300 c.e. and rediscovered by Girard Desargues and Blaise Pascal in the 17c. Projective geometry was discovered after Euclid, but Pappus and others determined that it was logically prior to Euclid. In other words, you can derive Euclid from projective geometry but not the other way around.

Lacan sought advice from mathematicians and carefully developed his thesis about projective geometry’s role in psychoanalysis during the middle seminar period, but many of these seminars have not been officially translated. The English translations from lecture transcripts made by Cormac Gallagher are serviceable, but there is scant evidence of the visual richness of Lacan’s presentations. Evidently, Lacan used drawings on paper and, when works of art were referenced, projected slides. In contrast to the Gallagher archive, the French editions are richly illustrated and in color.

Many Lacanians, even those revered as the most authoritative, either profess a distaste for Lacan’s topology or minimize its usefulness. A large number of those who accept topology as a Lacanian given nonetheless mistake the origins of history of it. While Lacan was clear and even emphatic that his topology came from Pappus and Desargues, a large number of Lacanian scholars continue to cite Euler’s treatment of the famous Bridges of Königsberg Problem as the origin of topology. It was not. Euler’s “solution” gave rise to graph theory, not topology. The topology cited in relation to this problem is Affine (“rubber sheet”) Geometry, which could be described as “Euclid without the angles and distances.”

Seminar XIV (The Logic of Phantasy) is replete with references to mathematics. Lacan jokes that he is demanding that we “take our slide-rules to bed with us,” asserting that the structure of sex can be known, and that it is mathematizable. In the slide-rule analogy, the unary trait is compared to the Autre and its relation to the objet a, related to the Fibonacci numbers (the Golden ratio), and linked to the logic of the torus.

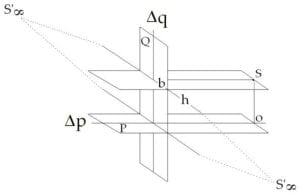
Seminar XIII (The Object of Psychoanalysis) is even more mathematically intense, with detailed excursions into projective geometry per se. In Session 18 (May 18, 1966) Lacan invited André Green and Xavier Audouard to give presentations; Michel Foucault was in the audience. The Gallagher translation provides almost none of the illustrations used by Lacan and his guests. With its intense visual effects, it is one of the most important sessions in what is key evidence that not only did Lacan “think visually,” but that he advocated a kind of visual methodology. Sessions 16 and 17 are essential for understanding what goes on in Session 18.

Lacan’s diagrams were not intended to illustrate but explain. They are a part of his theory about the subject, a topological protocol. We must remember that 2-d projective topology does not offer space for viewers to look at diagrams. What we see as a torus is not a torus but actually a 3-d immersion of the topological relationships that are the 2-d torus of the real projective plane. The fact of immersion is key. With immersion, we see non-orientation as a paradox, a kind of coincidentia oppositorum. This does not exist in the real projective plane, only in the perspectival space where we, as witnesses, notice the cuts, twists, flips, and folds of projective forms such as the Möbius band, Klein bottle, and cross-cap.

My thesis is that, to understand Lacan, we must understand projective topology, the topology of Desargues, Pappus, and the mathematicians of the 19c. such as Möbius, Riemann, Plücker, Gauss, and others who had discovered and revived Desargues’ and Pascal’s theorems. Whoever fails to understand topology in these terms has only limited access to Lacan’s thinking, and is in danger of misrepresenting the spirit of his œuvre. Any one idea in Lacan’s thinking is permeated with topology; it is impossible to ignore topology’s influence.

My project is to focus on separate session of unpublished seminars in the “middle period,” reproducing Gallagher’s English text but adding illustrations from the French versions. If necessary, I will correct spelling or add bibliographic or biographical footnotes. The aim is to provide readers with the visual materials that Lacan’s original audiences would have had, or that I speculate that they would have had, to make it possible for the first time for the English-only reader to see what he was talking about.

• Seminar XIII: The Object of Psychoanalysis (1965–1966): Restoring Session 13 (March 30, 1966)
  (Note: Gallagher left a note for session 13, saying that it would soon be restored to his translation, but that never happened. Read this stop-gap translation to see that Lacan’s topological thinking was indeed comprehensive and provocative.)
• Seminar XIII: The Object of Psychoanalysis (1965–1966): Restoring Session 16 (May 4, 1966)
• Seminar XIII: Graphic errors in the ALI edition of session 16.
• Seminar XIII: Restoring Session 17  (May 11, 1966)
• Seminar XIII: Ghosts that Tell the Future: This position paper shows how Desargues’ adaptation of Vignola’s “perspective hinge” develops a prismatic perspectivalism within ordinary percpetual experience.
• Seminar XIII: The Object of Psychoanalysis (1965–1966): Restoring Session 18 (May 18, 1966)
• Marc Darmon, “The Schemas R and I,” Essais sur la topologie lacanienne (translated)