 The Problems of the List
The Problems of the List
The Argentine poet and short-story master, Jorge Luis Borges, should be given credit for making famous the first connection between lists and projective geometry. In his 1942 essay, “The Analytical Language of John Wilkins” he presents The Celestial Emporium of Benevolent Knowledge (Emporio celestial de conocimientos benévolos) a taxonomy of animals. As the list adds an item, it changes its criteria for inclusion, in most cases suggesting new necessary categories based on binary logic (domesticated dogs to match stray dogs, for example), but such additions are provocatively obviated by such items as “those included in this classification” and et cetera. In terms the Lacanian case of bi-univocal concordance, there is none. There is no index separating, on one side, a consistent use, meaning, or other criteria and, on the other side, an example or personification of that class. But there is still the idea of two bijective lists, although bijection is not just missing, it is forbidden. In its place is what is elsewhere called “the thesis of the polythetic set,” which allows the rules to change in midstream, and doesn’t blink when the effect generates the cause, or the example the category.
- those belonging to the Emperor
- embalmed ones
- trained ones
- suckling pigs
- mermaids (or sirens)
- fabled ones
- stray dogs
- those included in this classification
- those that tremble as if they were mad
- innumerable ones
- those drawn with a very fine camel hair brush
- et cetera
- those that have just broken the vase
- those that from afar look like flies
 The Chinese Encyclopedia demonstrates the power of polythesis vis à vis the Russell Paradox, which forbids a signifier to represent itself or a catalog pretending to be exhaustive to include itself among the list of books. In this thought experiment, the Paradox of the Paradox can be demonstrated by thinking of the Borromeo Rings of Lacan’s famous RSI system (the domains of the Real, Symbolic, and Imaginary) as both Euler rings (sworn to represent only “reality situations”) and also a Chinese Encyclopedia.
The Chinese Encyclopedia demonstrates the power of polythesis vis à vis the Russell Paradox, which forbids a signifier to represent itself or a catalog pretending to be exhaustive to include itself among the list of books. In this thought experiment, the Paradox of the Paradox can be demonstrated by thinking of the Borromeo Rings of Lacan’s famous RSI system (the domains of the Real, Symbolic, and Imaginary) as both Euler rings (sworn to represent only “reality situations”) and also a Chinese Encyclopedia.
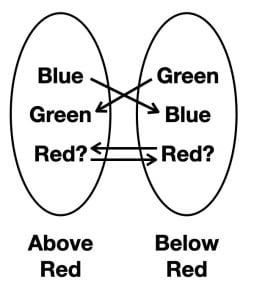
Imagine that you receive the Borromeo knot in an Amazon box and you unwrap it. There are instructions, with two lists. One list begins with the Red Ring and requires you to list the rings on top of it.Easy:
- Blue
- Green …
- Red?
Can a ring be on top of itself? Certainly if Blue is on top of Red, and Green is on top of Blue, then the next ring to note as next on top is the Red ring.
Not to worry, try another list, also from instructions in the Amazon box: “List the rings on the bottom of the Red Ring:
- Green
- Blue
- Red?
There are two problems: (1) the Russell Paradox problem of including the Red ring in the list of rings on top of the Red ring; and (2) the seeming impossibility of a ring being on top and bottom of itself. This, roughly, is the problem James Joyce construes in a puzzle involving Hamlet and his father. In his first major novel, Ulysses, Stephen Daedalus’s boisterous boastful friend Buck Mulligan, mocking Stephen, tells their mutual friend Haines that Stephen “proves by algebra that Hamlet’s grandson is Shakespeare’s grandfather and that he himself is the ghost of his own father” (Ulysses, 555-57). The characterization comes from the arch-skeptic Mulligan, and skeptics are the official proclaimers of confusion.
In the Dalkey episode, where Stephen is teaching a class of boys he wishes to baffle, he presents riddles missing key points of information. In Ulysses, he gives his class boys a riddle to unsettle their minds before dismissal:
The cock crew,
The sky was blue:
The bells in heaven
Were striking eleven.
“Tis time for this poor soul
To go to heaven. (U2.102-07)
The “answer” given, which satisfies no one, is another puzzle: “The fox burying his grandmother under a hollybush”—Ulysses, 2.115). Foxes are known for digging up carrion, not burying respected family members. The holly is an evergreen, symbol of eternity, which may apply to the instance of the fox’s backward behavior or the whole riddle. This alerts us to the anomalies of the riddle itself: dawn is breaking but the bells are striking eleven, the last hour before noon, antipodal to the first hour of day (or last of night, when the sky is blue and cocks crow before the sun rises). The time when souls go to heaven, what “time” would that be then? This is further complicated by the second version Joyce gives in the Circe chapter:
The fox crew, the cocks flew, The bells in heaven
Were striking eleven.
Tis time for her poor soul
To get out of heaven. (Ulysses 15.3577-81
She’s in she’s out. She’s his mother, she’s not his mother. It’s around 5 a.m. but it’s just now 11. She’s dead but the holly is eternal. Just as the Borromeo knot presents its riddle in two separate riddles — what’s above me? and what’s below me? — with the Russell Paradox to join them, Stephen Dedalus’s antipodal twins have problems of self-inclusion. This is not just circumstantial, but it should be noted that Mulligan has mocked Stephen for his insensitivity to his mother’s recent death. He cannot lay her soul to rest; he is the fox who will be compelled to dig up her bones, but 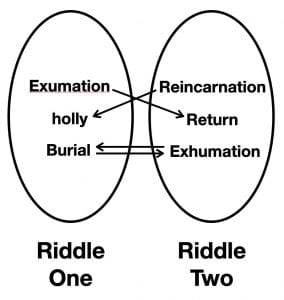 in digging them up he will reconfigure her corpse by scattering it, as the fox does, throughout the text, which will be “in its bones” a maternal speech. What is the material speech? Stephen’s twinned riddles and riddles with twinned contronyms (5/11, digging-up/burying, going to heaven versus going out of heaven) pairs resurrection with the dial of the clock and the half-circuit that separates melancholy down-dawn with the apogee of noon. 180º are also the cycle of life and death in resurrection, 180º apart in the binary of life and death but 360º as a circuit of the Eternal Return. The fact that Joyce has repeated the riddle twice implicates another survey of the circuit, 720º.
in digging them up he will reconfigure her corpse by scattering it, as the fox does, throughout the text, which will be “in its bones” a maternal speech. What is the material speech? Stephen’s twinned riddles and riddles with twinned contronyms (5/11, digging-up/burying, going to heaven versus going out of heaven) pairs resurrection with the dial of the clock and the half-circuit that separates melancholy down-dawn with the apogee of noon. 180º are also the cycle of life and death in resurrection, 180º apart in the binary of life and death but 360º as a circuit of the Eternal Return. The fact that Joyce has repeated the riddle twice implicates another survey of the circuit, 720º.
In the second form of the riddle, the fox is crying, the cocks are flying, the bells complining (Complines is a prayer usually said at 9 p.m., before bed, but the bedtime of the day might be described as the eleventh hour). Midnight is the classic moment for the release of souls, Walpurgisnacht, April 30/May 1. Joyce’s riddle is given in two parts, each with its own jagged fracture line; in other words, it is a tesseræ, meant to be rejoined, just as the two ovals have voids that are symmetrical.
Is this the logic of the Chinese Encyclopedia? Is any list not inherently “non-orienting” in that a species does not fit within a genus without giving up something? And, if that lost element remains, as the jagged edge of the tesseræ half, is there not a “destiny” to be lived through some kind of causal agency that is virtual to the standard cause-and-effect linear model?
It is certainly tempting to recall the function of the thaumatrope, the ancient disk spun on a fiber chord to rehearse the death of an animal of pray in advance of the hunt. The hole of the ancient thaumatrope was in the center, a void shared with the vector of the spear of the kill, which the chord “eternalized” with its successive replay spins. The visual result of the thaumatrope was, thanks to the Ø function producing virtual motion from two
still images alternated faster than the neural threshold for detecting flicker, argues that homeostasis/idempotency is the motive behind the hunter’s rehearsal, that death should be brought within the compass of life rather than allowing it to construct an impasse. Ernst Jentsch’s dyad of the uncanny, the cross inscription of Dead and Alive as Da/Ad comes remarkably close to qualifying Joyce’s two riddles as both a thaumatrope and non-bijective union without intersection.
Can we return to the case of the Borromeo knot? In the command to list what is above and below, we find echoes of Joyce’s use of the clock face’s nadir and zenith, as well as life’s nadir of death and zenith of resurrection (“Tis time for the pour soul / To get out of heaven.”). The key to lists may be that one list always implies a second list, but with the missing elements reversed. This is precisely the definition of Lacan’s Euler circles that overlap to create a union without intersection, manifest by the lozenge-shaped void of the impossible (but, by the same token, Real). In the criss-cross relations that spin issues of burial and reincarnation, morality of the corpse and immortality of the holly tree, and the binary actions of burial and exhumation (otherwise why choose the fox as undertaker responsible for proper burial?), the Chinese Encyclopedia, too, spins its list of improbable species, not so much monsters in themselves as animals made monsters for the (failed) cause of enclosure.
The problem of the list is two-fold. Can a list include itself as a part of the list, especially if it proclaims itself to be exhaustive? And, does a list impose a uniformity that is unproved and must be accepted as axiomatic. This is a problem with the messages that shoot back and forth between the Lacanian subject, whose speech and especially repetitions constitute an ambiguous demand (which focuses on objects and services but which is always about something else), and desire, which is something that comes from the Other in the form of an ambiguous expectation, requiring the subject to ask Ché vuoie? — “What do you (really) want?” A list can be an inventory, a set of instructions, a sequence of temporal events, or points of an argument or thesis. Lists emphasize sequence and consecutive order. They imply completeness, like a list of assets that is a legal requirement in valuing an estate. Despite the variety, however, lists are inherently bijective (1:1) in the sense that any list we make implies an ideal list as its model. The “check” list follows the 1:1 regimen on behalf of its presumption of adequacy — that it can successfully fulfill the ideal list’s obligations, to be complete, and in the correct order. But, lists will inevitably fail the bijection test. Even when they are “meroic,” a list made as an analogy of something else known to be complete, such as the human body, the Russell Paradox involving self-inclusion and the kind of non-orientation that would be encountered if we made a list of the box of rings in the Borromeo Knot Kit from Amazon would win in the end.
In the following lists, from Harold Bloom (about anxiety), Henry W. Johnstone, Jr. (on travel), Jacques Lacan (psychoanalysis), and Jorge Luis Borges (categories of the fantastic), non-orientation and self-intersection problems not only abound; they define these lists as “great lists” because they directly address these issues of non-bijection. They allow the problem to determine the nature of the list as a whole and the particularity of items in the list, as well as their interrelations.