
The idea of a thinking machine draws from the tradition of the ancient zairja (ةجرياز), an actual device that existed and was described by Ibn Khaldun (1332–1406), the Tunisian–Andalusian historiographer and economist. It is likely that the Catalan mystic Ramon Llull (1232–1315) contributed to and was influenced by the astrology of the zairja. How the zairjas worked is not entirely clear, except that the main aim was not to clarify thought but to confuse it. Combinatorial diagrams cross-pollinated ideas so that their inner forms became visible. An “agutezza” figured as (Stoic) animus was distilled and extracted.

Some have characterized the zairja as a kind of “reverse computer.” Instead of compiling data to be reduced to more determinative structures, the zairja used celestial calculations and aleatory procedures to extend potential and sometimes fantastical relationships, specifying as many causes as possible for any one idea or effect. Most historians presume that the Catalan mnemonicist–mystic Ramón Llull, whose theories were taught at the University of Paris until the 1500s, based his Ars Magna (1305) on the zairja and intended his combinatorial diagrams to work in the same way, with the aim of spiritual perfection.2 It would not be an exaggeration to say that a computer, albeit the zairja’s reverse–causality computer, lies at the foundation of Western thinking!
Can the confusion the zairja seemed to promote be productive? Leibniz (New Essays on Human Understanding) thought so:
Confused thoughts often make themselves vividly sensed, whereas distinct ones are usually only potentially vivid : they could be actually so, if we would only apply ourselves to getting through to the senses of the words or symbols; but since we do not do that, through lack of care or lack of time, what we oppose lively sentiments with are bare words or at best images which are too faint.
The zairja attempts to correct the “bare words” or “too-faint images” with a procedure of exactitude. At every randomly encountered vivid-but-confused thought, a turn must be made from issues of meaning at the level of the sentence (phasis) to meaning constructed out of style (lexis). The critical issue is that of voice, which is normally regarded as secondary for the speaking being; but it is this very secondariness that, within speaking, installs an anamorphic function that equalizes the “chance” of meaning with its “necessity.” Because necessity follows rules of diachrony, moving from the beginning to the end of the sentence, while chance locates itself at the vertical axis of metaphoric replacement (hence, choice) in that sentence, the zairja regards the intersection as point through which all vectors must pass. Just as Fibonacci discovered how a ratio necessarily involved equalizing the container and the contained (Lacan: éxtimité), what Leibniz called “blind thought” is a point deepened by the anamorphosis of the voice, which is first manifest through style, lexis.
This seeming accessory to meaning becomes a hinge, a pivot, a spin function. This strategy, seemingly ersatz, is generative. Just as hypnosis opens up the subject to an interior passivity lacking resistance to the voice of the hypnotist, zairja paralyzes the (pretended) function of choice and automates voice as instruction, although the origin of this voice is local: autodidaction.
illustrating the zairja principle as “the one of one”

If the mysterious length of the mysterious “golden” rectangle is x, the 1×1 square beneath the larger segment is unary but not a unity. It is both less than the area of the (golden) rectangle that encloses it (x • 1), and greater than the square that is the next-largest space adjacent (x–1 • x–1). This “both < and >” status qualified it as a kind of ring that is found in the Borromeo knot, any one of the three rings is both on the top and bottom of a stack, although to be clear, the golden ratio serves up a stack of spaces that is orientable, since the innermost infinity stays on its side of the 1•1 square; the outermost, proceeding “outward,” with larger and larger rectangles, from the 1 • x shown in the illustration.
While the golden rectangle is not self-intersecting, as the Borromeo knot is, it is not officially a projective surface, but it manifest the difference between unity and unary that is critical to understand the zairja. While a unity would resolve the value of Ø as a real number, the Fibonacci series
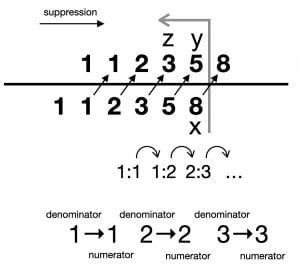
, as is well known, refuses to do this. The series, 1, 1, 2, 3, 5, 8, 13, 21 … etc. does demonstrate the property of self-intersection that the graphic golden rectangle does not, when each value is “jogged over” one interval to create a series of fractions: 1/2, 2/3, 3/5, 5/8 … — a series that trends towards the value of Ø.
A graphic of this process reveals how Dante’s terza rima thinking (ABA, BCB, CDC …) uses a linked chain strategy to approach a unary end that is not a unity. For Dante, this was 100, but in the same way that the series 1/9 (=.111…), 2/9 (.222…), 3/9 (.333…) reaches a “1” that is both 1 and not 1 (.999… by extension of the pattern of division).
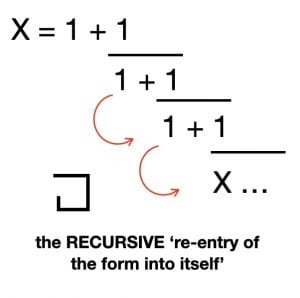
As a graphic, this fractional approach to the value of Ø shows how a numerical terza rima involves the bar of division in several distinctive ways. The most important for the zairja’s use of the unary trait is that if suppression. In a fraction, a number is written, “X” for example, but what is suppressed is the value of itself, which can be

written X/1. “One X” might be one way of vocalizing this. In an energetics model, suppression would require a response, an expression, where the suppressed value would, in a second iteration, be in the position of a numerator, which would in turn “suppress” its own denominator. This is what happens, literally in the series 1/2, 2/3, 3/5 … etc., with the “self-intersecting” feature, that each new suppressed value is the sum of the numerator and denominator in the previous iteration.
This may seem to drift quite far from the idea of the zairja, but in effect the idea of the — of the iterations that, continued to infinity, with Ø as a vanishing point on the horizon, qualify the golden rectangle as a 2-d surface that has, like the Borromeo rings, immersed itself into 3-space, with the same irrational result, Ø, thanks to a bar that mediates both suppression and expression. The < and > of the 1•1 square in Fig. 1, the centrifugal trend toward two antipodal infinities, great and small, becomes the >< of increasingly accurate measures of Ø if we treat X as a unary value, X/1, what comes “just after” — > — the 1•1 square — and take the next smaller space as a “just before” (Fig. 3), “suppressed” by the central area of the square.
With the repression/expression function of the bar in the series 1/2, 2/3, 3/5 … , it is possible to see that the unary trait is self-intersecting and non-orienting (Fig. 4). As both self-intersecting and non-orienting (i.e. the irrationality of the number Ø), the golden rectangle is, like the Borromeo knot, a demonstration of the unary trait, Lacan’s version of Freud’s einziger Zug. What does such a mathematical concept have to do with what, in the psychoanalytic clinic, is a universal symptom?
At this point, the zairja idea becomes critical. The metrics of the golden rectangle connect to the idea that the zairja is, essentially, a computer, but the first zairja’s were astronomical/astrological and diagrammatic. Is it possible to say that the “self” of the zairja is somehow equivalent to the “self” that inserts the value of the question into the answer (and vice versa) in the case of the golden rect
angle? It is necessary to involve the multiple functions of the bar in psychoanalysis. At a rudimentary level, the bar is the division between the Subject’s consciousness and unconsciousness, so we must add that the bar exists only for the neurotic subject, the only class of subject that has a demonstrable unconscious. (Psychotics and perverts cannot be said to have an unconscious, at least not in the same way as neurotics, because of their relations to the Symbolic, to language.)
Another function of the bar is that of repression, similar to the mathematical demonstration of suppression of a denominator in the demonstration of the difference between “unary” and “unity.” The idea of unity is convergent and determinative. “Unary,” in contrast, is dispersive and indeterminate, transporting a ratio, x/y, to every point on its “surface.” The unary is primarily a self-intersecting, non-orienting 2-d surface, whose topology is evident in the zairja’s logic of displacement and condensation — the same forces that, Freud argued, constitute the logic of dreams.
Emergence
In zairja, the concept of an individual consciousness does not exist. At minimum, and as a model for larger collectivities, the barred Subject, $, stands in relation to a constructed Other, both as an Autre and as an “object–cause† of desire,” Lacan’s famous objet petit a. The Unconscious is the locus of this Autre, where the repressed resides in a continual state of potential return, an anamnesis. The classic demonstration of emergent intelligence is the discovery made by Francis Galton in 1906, when he discovered that the unsuccessful guesses of the weight of a prize ox, if added and averaged, revealed the accurate number. Given that no one “knew” (in the traditional sense) the exact weight, this result must be said to be a case of kenosis — “knowing without knowing,” simultaneously emergent and collective.
The working zairja must, therefore, aim to be collective in some sense (involving a “dispersed” series of unconnected elements). Its “unknowns” must be, at the level of the individual, “un-knowable,” adding to the definition of the unconscious as un-conscious, the essential element of the group, present in the form either of dissociative structure (randomization) or participatory enactment. In Galton’s experiment, the unary trait was the precise weight of the prize ox, not as measured by the scale but as guessed by the collective of mistaken hopefuls. Neither collectivity nor despair/ignorance can be removed from the zairja’s “algorithm.”
Freud’s einziger Zug, the “sign of the Other, of which the Other is unaware,” reveals the logic behind S(A), the signifier of the lack of the Other. Since the Other is defined precisely in terms of a lack which “resides” in the Other’s Unconscious, we see a means of relating the zairja, primarily a device of the Symbolic, to this structure of the Unconscious as Other, and Other as Unconscious. In fact, it is to this double sense as well as to the chiastic, cross-inscribed relation of the Other to the Unconscious that the unary trait’s meaning becomes more clear. The consolidated glossary of the online resource, Psychoanalytic Electronic Publishing (PEP-web) writes:
For Lacan, that which Freud termed identification is an effect of language, that is, the constitution of a subject by the incorporation of signifiers. Different types of otherness correspond to different types of identification, three of which are found in Freud; the otherness of the Father (a mythical identification, according to Lacan, since it precedes any libidinal investment); the otherness of a primary trait of difference (identification with what Freud calls the unary trait — Einziger Zug — as the basis of the constitution of ideals); the otherness of the Imaginary other (narcissistic identification founded on the image of the body and on the experience of fellow beings); and the otherness of the object, in so far as the object is the cause of desire (a paradigmatic example of an identification with the *object is the relation of a melancholic subject to the lost object). The subject that psychoanalysis is concerned with is by definition an other and is therefore always taken for an other.
Otherness, the essence of the zairja as an “anti-computer,” extends the unary trait so that “the different” (the distinction, distilled as a minimum) becomes the basis for the same, i.e. identity, especially identity in the face of the lack of support by any system of semblance, association, or structure. Idem-potency, this power to remain the same in the face of a lack of any basis of the same is, geometrically, the golden rectangle and, topologically, the Borromeo knot.
†For Lacan, “cause” was an idea tempered by the slight-of-hand idea of causerie. As Ben Hjorth has written, “To be no longer master in one’s own house means to cease to (act as if one could) be the undetermined, ‘efficient’ cause of consequent effects in that realm.” As Rebecca Comay has put it, “[t]he aptly named chain of signifiers is anything but uncoerced.” Responding to this coercion rather than swallowing cause as as an unquestionable logical sequence becomes, for Lacan, more important than the conventional accepted idea. Wherever we see the expression, object-cause of desire, we must expect a con, a grift, a scam is going on.
See: “Zairja Thinking: A Second Virtuality for Design,” presented at the ACSA annual conference, remote zoom session held in lieu of San Diego conference, Spring 2000.
For a way to construct zairjas with others, apply these guidelines to Zairja as a Collective Project.
See also: David Link, “Scrambling T-R-U-T-H Rotating Letters as a Material Form of Thought,” Siegried Zielinski, Silvia Wagnermaier, and Gloria Custance, Variantology: on Deep Time Relations of Arts, Sciences, and Technologies (Köln: W. König, 2005), 215–266. The characterization of the Zairja as a “reverse computer” is a broad claim. The temporal reversal of the relationship of cause and effect is “forensic” in a way familiar to detective stories. But, there is also an emphasis on the signifier as prior to the signified, a kind of idealism that allows signifiers to visit then depart their signifieds, remaining intact until the next instantiation. This notion has been developed in detail in Jacques Lacan, “Seminar on ‘The Purloined Letter’,” Écrits: The First Complete Edition in English, trans. Bruce Fink, in collaboration with Héloïse Fink and Russell Grigg (New York and London: W. W. Norton & Co., 2006), 6–50.