quick links
- The Workshop Idea
In Lacanian studies, the question of clinic v. culture are a Scylla and Charybdis. The workshop idea is purely structural, purely pedagogical. It is a design that others can follow (voluntarily, when opportunities arise) to introduce a third “clinic” where topology is brought in to study a work of film, art, literature, using the occasion offered by conferences. The Third Clinic is the Clinic of Ethnotopology. It’s grounding principle is the relation of inversion and induction to topology. - The Cathedral Workshop
Topology Pirates! Propose a workshop for your next conference with at least two Lacanian topologistas and help spread the New Lacanian Topology based on induction and inversion. Read Raymond Carver’s short story, “The Cathedral” to get a head start. - Lacan’s Pre-Torus Topology: Žižek’s Bluff about the Double Frame
We knew it wasn’t true … Žižek did not invent the double frame out of thin air during a boring academic conference. It’s not only been around for a while, it is the idea of the “inside observer,” critical to 2d topology. - From Knowledge/Truth to the Torus
When did Lacan start to think about topology? Don’t swallow the historicist’s account. It started when Lacan decided to be Lacan, much earlier than the official date, Seminar IX. This earlier essay tries to get at the big picture by aligning presentation with the subject and demonstration with the signifier. - Recent videos on topology, in English and Farsi
Watch recent videos on YouTube, with translations narrated by the velvet voice of Iraj Ghoochani. - Why should the Borromeo knot be anything other than the Real, Symbolic, and Imaginary? How about this: Marriage, Hygiene, and Paralysis [under development … come back after April].
Many Lacanians face Lacan’s topological theorizing with a mixture of hope and existential fear and trembling. Not many Lacanians are well-enough educated in mathematics to grasp what Lacan is saying about topology. His array of toruses, cross-caps, Klein matrices, Borromeo knot variations, the loops and stitches of his Graph of Desire; and the diagrams of projective geometry puzzle the majority of Lacan’s earnest followers, who seem not understand Lacan’s claim that, by the Real, he means structure and by structure, he means topology.
Writing that directly addresses Lacan’s topology is curiously crippled by misreadings of mathematical history. Lacan seems to have done his homework. In Seminar XIII, The Object of Psychoanalysis, he identifies the founders of projective geometry, Pappus of Alexandria (300 c.e.) and Girard Desargues (who worked with Blaise Pascal in the 17c. to revive interest in Pappus. Their work was dismissed and forgotten until the 19c., when it was revived and made the core of a century of glorious advances in geometry, thanks to mathematicians such as Gauss, Plücker, Möbius, Riemann, Boys, Klein, and Hilbert.
However, Lacanians frequently dismiss or misconstrue this history. They do not read what Lacan has to say. Instead, many respected Lacanians regard Euler’s Königsburg Bridge Problem as the origin of topology, when in fact it is the basis of graph theory, not topology. “Rubber sheet topology” is not projective topology either. That is affine geometry, which is Euclid without the distance and angle measures. Projective geometry is about forms that do not have any visual presence for us. To see them, we must “immerse” them into three dimensions, where their cuts, twists, pokes, and folds will be visible to us even though they don’t technically exist in the smooth planar situations of what’s called the “real projective plane.”
Without Lacan’s topologies it will be impossible to have any full understanding of his concepts. But, while Lacan is what we might call a “visual thinker,” most Lacanians are not. Visual examples are not just useful for understanding Lacan. They are essential. Visual materials do more than supplement the text. They show what is happening. They allow us into Lacan’s process-intensive thinking. Visualization serves not simply to provide analogies or illustrations; it is a way of thinking into and beyond Lacan’s materials, which stop at the mi-dire point intentionally, as an invitation for theory to work beyond the givens.
Inversion and Induction

In a 2023 seminar on Lacan’s “La troisième,” Iraj Ghoochani observed that Lacan’s transformation of the Borromeo rings into a circle (for the Imaginary) and a cross (the Real and Symbolic) was both a Brunnian conversion AND an inversion circle transformation. Any ring inside an inversion circle translates to a straight line whose ends, formerly at the center of the circle, are then at infinity. The Imaginary, tangent only to the circle itself, remained a circle. The otherwise able translator of “La troisième,” Yolande Szczech, had defined the R and S lines as “Cartesian,” an unlucky guess. Presuming that Lacan had understood this conversion was based on the fact that the circle defining his idea of extimité is, in fact, an inversion circle, we applied the rule of inversive geometry, that what is inside the circle is equivalent to what is outside. This balance seemed to conform perfectly to Lacan’s contention about the relation of the unconscious in relation to the neurotic position within the Symbolic (and therefore “acting out”) to the position opposite on the fundamental polygon of the torus, the “I think not” position of psychosis outside the Symbolic and, hence, position in relation to the passage à l’acte.
Inversion made sense not only of the new RSI as a “dial” of the Imaginary, comparable to Peirce’s dial of the square of oppositions, adapted by Lacan by “detaching” the position of the universal negative, but also to Lacan’s revised reading of the discourse mathemes, defined by jouissance and surplus jouissance. Goochani’s discovery seemed to open many doors at once. The next step was to see how inversion extended Lacan’s topological thinking. Inversion seemed to affect both his later thinking about jouissance in relation to the “energetics” of circuits defined by knots, but also to earlier thinking, even to the Three Prisoners’ Dilemma, where a cut divided a space logically into two equivalent halves.
At this point, the connection of inversion to the induction puzzle became obvious, if for no other reason than the fact that the Three Prisoners’ Dilemma is a prime example of induction, where a defective instruction contains its own solution. The faulty instruction in this case is the rarely noticed fact that the Warden implies that there will be only one winner, while his use of three white dots precludes this. The prisoners, all of whom see two white dots, know immediately that it will be impossible for ONE of them to win, because only a view of two black dots can conclusively determine the remaining prisoner’s dot color.
The defective instruction is also native in Lacan’s thinking, as his mi-dire style of speaking and writing. As an induction puzzle, the aim of this style is clear: to compel the listener/reader to apply the same logic of self-intersection with non-orientation that applies as the geometrical principle of his 2d topological examples: the torus, Möbius band, cross-cap, and Klein bottle.

Inversion and Induction quickly became a new way of theorizing Lacan’s topology, showing that his interest in self-intersection and non-orientation extended far beyond the conventionally assigned confines of the middle seminars. The real payoff of this insight is, however, the fact that inversion and induction are the logics by which cultures structure rituals practices, games, religious beliefs, myths, folktales and, later, the putatively more sophisticated products of the arts, literature, architecture, music, etc. We could even say that all objects, even those regarded as purely utilitarian, have an inner inversive/inductive economy. Wherever there is exchange and limit, inversion and induction are there to regulate the flows, the resistances, and the insulation that define the space and time of activities and transgressions.
This is a new way to look at Lacan, where mathematical topology is optional, because it is already present in the operations of inversion and induction, as these are present in every cultural object and operation. Thank you, Iraj!
The Premise of the Workshops
The strategy of this sequence of workshops is to begin with the central role of the unary trait, the root of Lacan’s idea of the signifier, the symptom, and metaphor. Rather than theorizing abstractly, the strategy will be to choose works of literature and film where the rule of the unary trait can be clearly documented, then to gradually extend the unary trait’s functionality to the topology of the torus, in both its “immersed” 3d forms and its 2d structure, made explicit by what is known as the “fundamental polygon” diagram, which Lacan used extensively in Seminar XIV, The Logic of Phantasy.
The wager is that, if one can understand how enjoyment enables the effectiveness of the work of art, one can understand the topology. With structure as the means of extending the logic of the unary trait, topology can be seen as a fifth “Aristotelian cause,” grounded in what Lacan called the failure of material cause — its passivity. Key to this wager is Slavoj Žižek’s idea of the “reality of the virtual” as the element of effectiveness within each of the three Lacanian domains, an effectiveness of the Real, the Imaginary, and the Symbolic. In effect, Žižek has proposed a way of understanding topology through anamorphosis — what can be seen but is not seen; what can be heard but is not heard.
These workshops are inspired by a Lacanian friend, Prof. Sheldon George. Like many Lacanians, he senses the need to understand topology in a functional way that benefits both theory and clinical practice. Ultimately, Lacanians need to define what jouissance is for theory. Is it a phenomenon to be studied abstractly, or is in at active ingredient in the strategies required for psychoanalysis to achieve its goal of being a “science of the subject”?
Somerset Maugham’s Mr. Know-All

In this short story written in 1924, the narrator dislikes Max Kelada, jewelry trader and self-proclaimed expert on almost everything. So do the rest of the passengers on the crowded ship from San Francisco to Yokohama. Although the racism implicit in the portrayal of Kelada as a “Levantine” seems to be the theme, the story and film focus on a secret held by a seemingly innocent passenger, Mrs. Ramsay, whose fate falls in the hands of the seemingly insensitive “Mr. Know-All.”
Although the decisive scene lasts only two minutes in “real time,” over half of the text is devoted to describing it, and the film must pack 82% of its time with supporting scenes to make sure that, in the remaining 18% taken up by this critical event will be understood fully, in terms of structure.
Read the clean text of the story, then the annotated text. At the same time, watch Ken Annakin’s 1950 film, a part of the Trio series that included two other Maugham stories, “The Verger” and “Sanatorium.” Then, watch the YouTube presentation linking the Unary Trait to the toroid logic the Mr. Know-All’s rescue of the (comparably) innocent Mrs. Ramsay.
Topology Basics and the Unary Trait
To prepare for thinking about the story in terms of the unary trait, read this short essay on “What Do ‘Self-Intersecting’ and ‘Non-Orientable’ Mean?” These two properties characterize projective forms. Without them a form is not projective, not topological in Lacan’s sense, and most important not related to the unary trait. Self-intersection is the principle of the circuit. In Freud/Lacan as well as physics, there is a principle of the conservation of energy. A circuit moves energy without gain or loss of energy. Lacan’s Graph of Desire seems to offer one picture of the principle of conservation. All of the psyche’s various checks and flows, its layers and inner circuits, must obey this law. The goal and aim are also a circuit obeying the rule of conservation. And, the retroaction of language and trauma are the essence of the idea that nothing is lost.
Self-intersection, like self-reference, produces conditions of non-orientation, as with the case of the logical circuit created by the Cretan Liar. “All Cretans are Liars” is, for the Cretan who utters this line, a conversion of time to a binary (non-orientable) temporality of T/F/T/F…. The Mirror Stage itself, with the production of two competing realms that, by being halved, contend for the territorial completion of the 360º horizon. Because the mirror is a cut rather than a reflection, there is no third, mediating space between them, only a Möbius band void of two inward-facing surfaces, non-orientable and self-intersecting.
Even the après coup of language is self-intersecting and non-orientable. If these principles represent topology as the structure of the Real, one could say that topology extends at least as far back in Lacan’s thinking as the Mirror Stage, and the metaphor of the stage is also a means of staging the metaphor, where the proscenium cut also produces the two overlapping claims, of the audience and actors, an overlap that is a void.
These two principles of conservation of energy show how to enlarge Freud’s idea of the circuit to include the all-important functioning of the death drive “in the midst of” the pleasure/reality regulative principles. The death drive is, in effect, a perpetual motion machine within an expenditure protocol. It promises to create a laminar flow between seeking satisfaction and achieving dissatisfaction, a way of freezing, negating, folding, or reversing time, as the theme of Nirvana suggests. Here is the operating platform for the unary trait, which in its timelessness is able to “monetize” retroaction on behalf of Effective Cause. This is the “payoff” in the work of art, which always begins with costs of strangeness, paralysis, and mortification. In “Mr. Know-All,” all of these elements can be charted and defined.
The Unary Trait
The unary trait is, for Lacan, the elementary form of the signifier, a kind of primitive substratum that lies both the historical and logical origin of language. This foundational aspect means that, while we can derive other functions of language and psyche from it, we cannot derive the unary trait from them. Its logical structure is autonomous and original, so we have to work with basic laws to deduce the operation of its fundamental parts. When Freud realized the importance of the einziger Zug, the cough that Dora had unconsciously copied from her father, he realized that the unary trait was (1) timeless, in that each instance of it was a kind of “reset” to a zero condition, and (2) logically reversed — neither Dora nor her father could be said to “have” a cough in the sense of an ordinary symptom; rather, “the cough had them.”
These two properties of time negation and predication reversal open the way to a new model of the unary trait in relation to the mathematical number, the 1. The 1, remember, is not a number until the number 2 is reached; then its status as a number is realized retroactively. Already the 1 involves time retroaction, a laminar flow binding two temporal vectors. Already there is a cut between the vectors that, like the mirror, creates Möbius-faces that are self-intersecting (conserving energy, a circuit) and non-orientable.
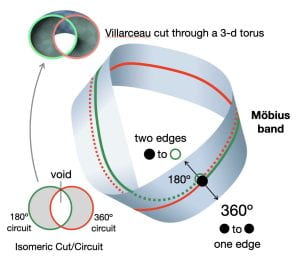
Review this short essay on the unary trait before beginning your analysis of “Mr. Know-All. It concludes by consolidating the Möbius circuit as self-intersecting and non-orientable to show how conditions such as symmetrical difference, the Villarceau cut, and the overlap of 360º/180º conditions apply to all signifiers but dominate the function of the unary trait. Here, we see a non-Lacanian term emerge: the “isomeric point.” This is a geometric extension of the idea of the unary, since it also involves the suspension of time and reversed predication. Its advantage is that it extends the idea of the unary trait to conditions in history and art, where the foundational logic of the unary trait works at the level of the signifier, with unexpected consequences.
The Isomeric “Point”
The mark on the Möbius band, which correlates to the cut of the Euler circles creating a void that “generates” a 2-d torus, is one of a set of related terms collected to projective geometry. In popular culture as well as psychoanalysis, the link between structure and material forms is immersion. While we can see Möbius bands, Klein bottles, toruses, cross-caps, and other examples of projective geometry, we cannot see their structure, which is purely two-dimensional. When we look at these immersions of structure into three dimensions, we must theorize how the 3-d features relate to the 2-d topological Real. We must learn how to see topological as anamorphic — belonging to two worlds.
The isomeric point heads the series on account of its role within the unary trait. The unary trait does not negate time as much as it diversifies it. Time in effect is spatialized. Within it we accomplish what Freud claimed in Civilization and Its Discontents was impossible: the ability to see Rome in all of its stages, buildings, fields, ruins all superimposed on top of each other. Later, in his essay “Transience,” Freud identified the opposite aspect of this paradox, the necessity of discrediting any single state of a temporal process — the woods outside Vienna, the Wienerwald was the example he used — as more representative than any other. Any person, landscape, or object subject to time was a lozenge-shape of origin, growth, maturity, and ruin. Transience complements the issue of conatus, the question of how identity survives continual change.
The great effort to see (1) amidst the universal condition of change, any possible constant or structure; or, conversely, (2) the fluidity of things that appear to be solid and unchanging; is the same effort required to understand the relation of 2-d topological structure as against its 3-d immersions. Six terms, isomerics, conatus, cathesis, the katagraphic cut, transience, and tesseræ are designed to ease this effort by locating aspects of immersion (into 3-d reality) and its converse, subversion (into pure structure), into works of art, everyday situations, stories, and jokes. This was Freud’s, then Lacan’s idea, of course. The aim of course is not to domesticate the unfamiliar but rather to show just how uncanny everyday experience actually is. Relations such as isomeric, conatus, cathesis, and transience; actions such as the katagraphic cut; and objects such as the tesseræ point to a science based on an anamorphology, where the Lacanian Real is present in terms of its effectiveness and structure. This is the meaning of topology, expanded through six bridge-terms.
Active and Passive: Zveckmäßigkeit
The German philosopher of culture Ernst Cassirer, like Lacan, saw that each signifier (“symbol” for Cassirer) miniaturized the logic of the entire Symbolic; this logic was split between a conscious intended meaning, consistent with collective use, and a suppressed content/function that was dialectically active. The relation was not perfect 180º opposition, but more like a 90º vector that could pivot between antagonism and sympathy. In Edmund Bergler’s theory of neurosis, aggression converts to humiliation, as if that had been its actual intended purpose. In an under-appreciated study of the hero, Irwin Cook argues that in classical mythology the hero’s trademark energetics of accomplishment is functionally twinned with a passivity that compels the hero to voluntarily face defeat. With literature and clinical psychology agreeing on this coupling of opposites, we must consider how Cassirer’s and Lacan’s idea of the signifier condenses this township at the most fundamental level of meaning.
One way of conceptualizing this problem is to focus on the function of metonymy, the form of metaphor that combines a “centrifugal” outward tendency to link with other signifiers and context with the emergence of a “centripetal” inner gravity. The most famous example is the case of Freud’s “Signorelli parapraxis,” where the Viennese tourist, trying to remember the painter he so admired during his visit of the Orvieto Cathedral, called up a series of names, places, and situations, none of which were the “lost name” of Signorelli but all of which had something to do with “signor” — what Freud saw in the painter’s name that native speakers of Italian would have ignored.
This is not the place to give a detailed account of this famous Freudian event. But, it is important to point out how the suppression of “signor” remained behind as a center of gravity holding in place the “centrifugal” proliferation of words that, although they were not metonymies in the normal grammatical sense, were function as metonymies in that they presented vectors at a 90º angle from each other, able to specify two spatialities, one topographical (as Freud traveled across the Adriatic), the other topological (the “landscape” of suppressed relations represented by Freud’s attempts to remember), at the same time.
